ピタゴラス音律、１オクターブは、CDEFG A B H（≠C）

きくずみん others 2023年3月12日 | 0

平均律は、異名同音

A＃＝B♭、C＃＝D♭、F＃＝G♭、G＃＝A♭

ピタゴラス音律

弦の長さ「3：2」の比率は、よく調和する（ドミナント）

弦の長さを３分の２にすると、周波数は1.5倍になる。（ドミナント）→ 上に完全五度（半音７個）

弦の長さ『3：4』もよく調和する（サブドミナント）

弦の長さを3分の4にすると周波数は０.７５になる→下に完全五度（半音７個）

→　完全五度を連続すれば、そのうち１オクターブの音階が作れる（はず）。

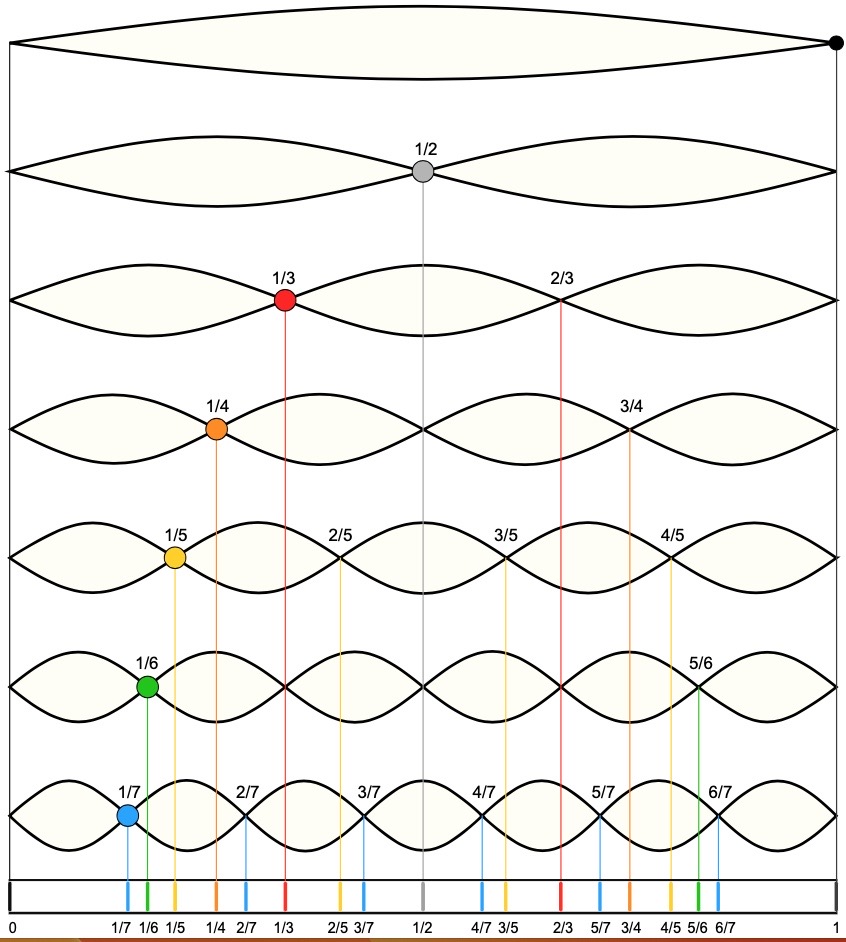
連続ドミナントで調和する音を作る

GのドミナントD、

DのドミナントA

AのドミナントE

EのドミナントB（＝H）

BのドミナントF＃

F＃のドミナントC＃

C＃のドミナントG＃

G＃のドミナントD＃

D＃のドミナントA＃

A＃のドミナントE＃（＝F）

E＃（F）のドミナントB＃（≠　C）

C →F

F→B♭

B♭→E♭

E♭→A♭

A♭→D♭

D♭→G♭

G♭→（C♭≠B）

B→E

E→A

A→D

D→G

G→C

３と４の公倍数の周波数で計算してみよう。